Binary Trees

Binary Tree:

 Binary tree is a special tree data structure in which each node can have at most 2 children.

Thus, in a binary tree, each node has either 0 child or 1 child or 2 children.

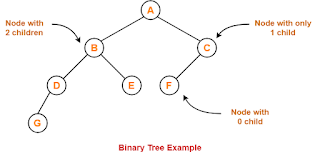
Binary Tree is a special type of generic tree in which, each node can have at most two children. Binary tree is generally partitioned into three disjoint subsets.

• Root of the node
• Left sub-tree which is also a binary tree.
• Right binary sub-tree

A binary Tree is shown in the following image.

Unlabeled Binary Tree:

A binary tree is unlabeled if its nodes are not assigned any label.

Example: 

Consider we want to draw all the binary trees possible with 3 unlabeled nodes.

Using the above formula, we have-

Number of binary trees possible with 3 unlabeled nodes

= 2 x 3C3 / (3 + 1)

= 6C3 / 4

= 5

Thus,

• With 3 unlabeled nodes, 5 unlabeled binary trees are possible.
• These unlabeled binary trees are as follows-

Labeled Binary Tree:

A binary tree is labeled if all its nodes are assigned a label.

Example:

Consider we want to draw all the binary trees possible with 3 labeled nodes.

Using the above formula, we have

Number of binary trees possible with 3 labeled nodes

= { 2 x 3C3 / (3 + 1) } x 3!

= { 6C3 / 4 } x 6

= 5 x 6

= 30

Thus,

• With 3 labeled nodes, 30 labeled binary trees are possible.
• Each unlabeled structure gives rise to 3! = 6 different labeled structures.

Similarly,

• Every other unlabeled structure gives rise to 6 different labeled structures.
• Thus, in total 30 different labeled binary trees are possible.